Japan (EN)
Select your region or country.
CNR(Contrast-to-Noise Ratio), eye versus machine.
THIS GUIDE IS FOR:
Persons who want to understand when their eyes may be misleading them
THIS GUIDE OFFERS:
A readable, yet rigorous discussion of the relationship between signal, contrast, and noise
Learn more...
Learn more about noise and CMOS technology, read Changing the Game.
For quantifying the ability of a camera to detect a signal (i.e., “Can I see my signal?”) and for defining the precision of the measurements made with a detector, the signal-to-noise ratio (SNR) of a camera is an extremely powerful tool. Yet there are cases when SNR cannot provide the most meaningful data.
Imagine a photograph of a cityscape on a foggy day. The image is bright and would likely have a high SNR, but our ability to “see” the skyline is impaired because of the lack of contrast. Contrast is a general term that gets to concept of “visibility”: Can I distinguish the signal of interest from the background signal? When we have an abundance of photons, i.e. in the shot noise regime, sensitivity becomes the ability to discriminate between two different, distinct levels of signal and in many cases the most important two levels are signal and background.
More than any other noise factor, background in the sample has been overlooked as a relevant term in considering sensitivity. This consideration is especially relevant for biological samples.1 We know that background affects SNR, but it also affects contrast.
Fundamentally, because of photon shot noise, wherever there is background signal there is also background noise, yet this also has a camera component. Similar to SNR equations, it’s possible to have contrast-to-noise (CNR) equations: CNR = QE * S / [Nb + Ns] where Nb is noise of the background and Ns is noise of the signal.
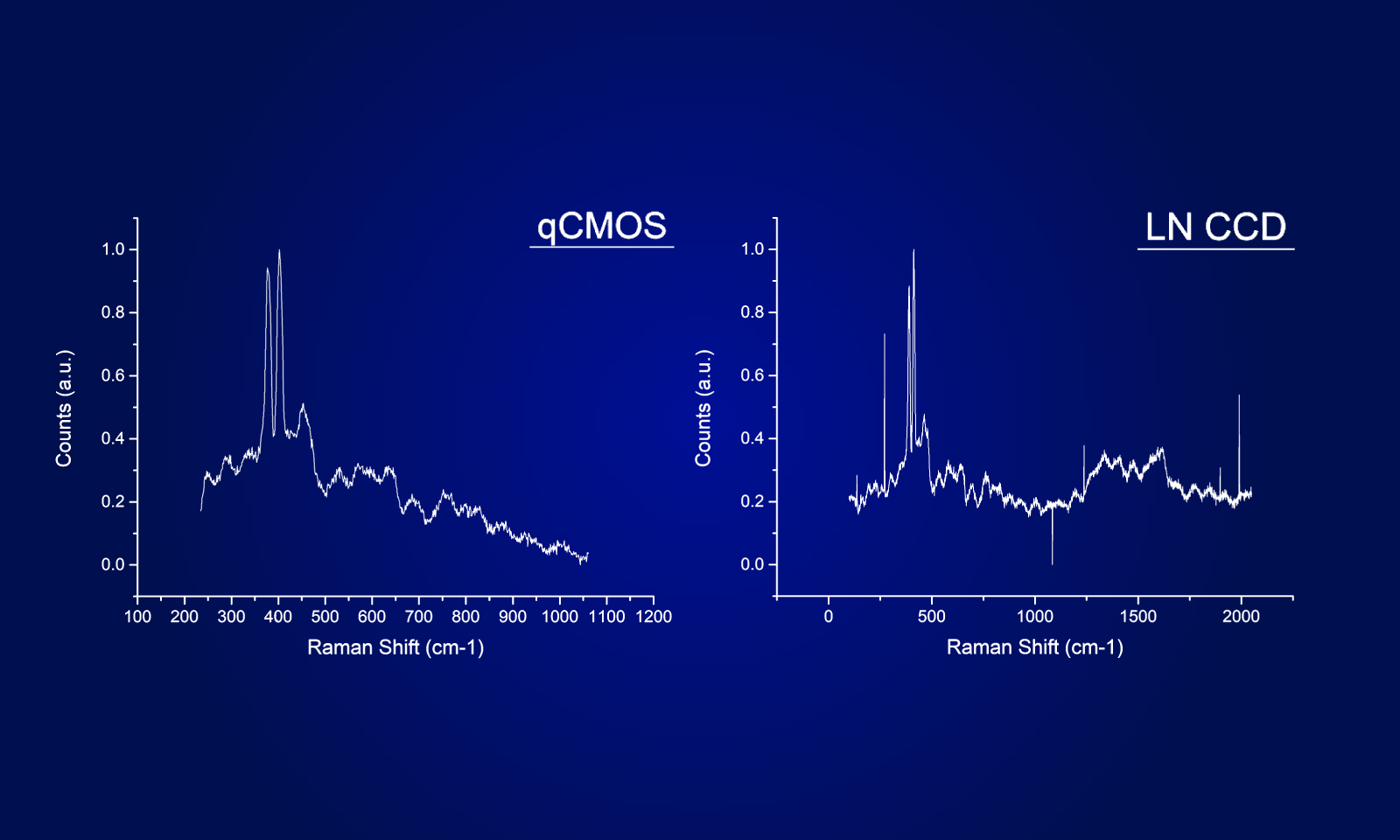
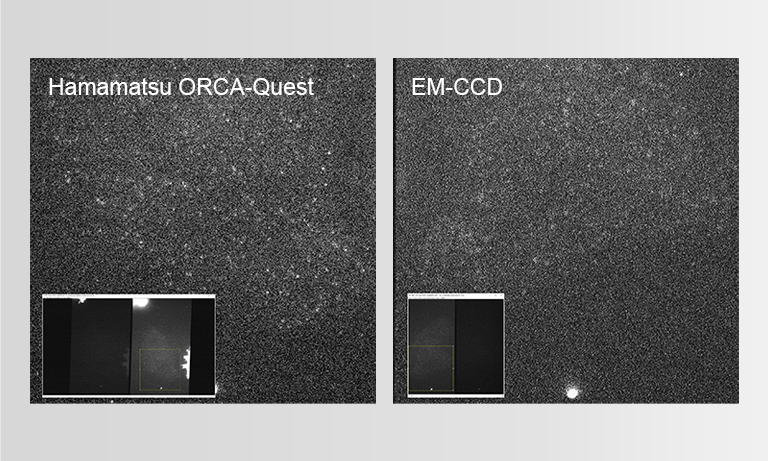
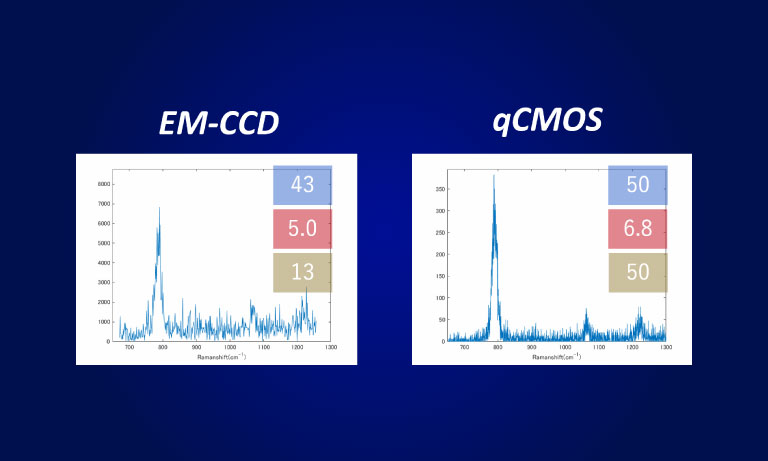
An easy way to visualize the difficulty that background and background noise poses in imaging is depicted in Figure 1. This figure shows that CNR is especially relevant when considering background in the context of choosing between an EM-CCD and the ORCAⓇ-Flash4.0 (older model of the ORCA-Flash 4.0 V3). We know that the cross-over intensity into the shot noise regime is a function of the read noise (Nr) of camera. Due to the great reduction in Nr with Gen II sCMOS cameras, in most fluorescence microscopy, both the signal and the background now reside in the shot noise (or eQE) domain. In this regime, because of EM gain noise (Fn), the noise of the signal and background detected with an EM-CCD will be higher than with the ORCA-Flash4.0 resulting in reduced CNRs.
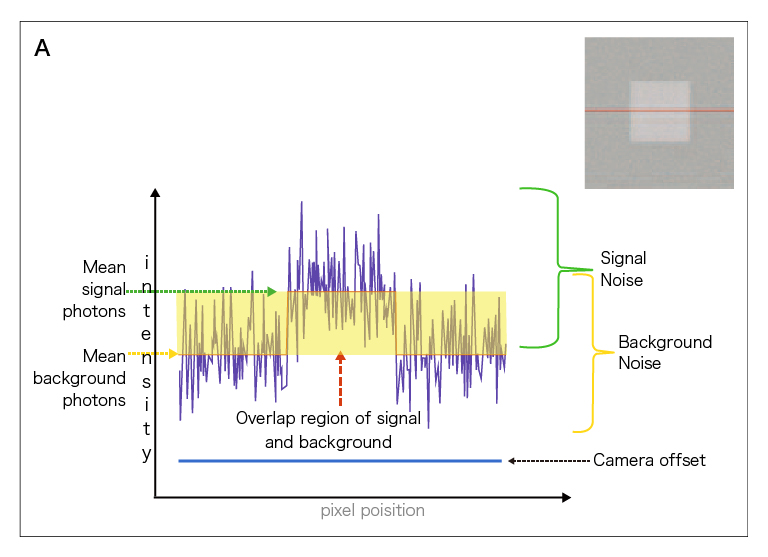
Contrast and noise. (A) The graph depict the signal intensity and noise of the line through the inset grey squares and demonstrates the problem with background in the context of contrast. Contrast in an image is the perceived ability to distinguish between the background and the signal of interest. If both were noiseless, this would not be too difficult even if the signal was nearly identical to the background. However, camera noise and photon shot noise create an overlap in the signal and background regions with similar intensity, making it difficult to separate signal from background.

(B) Because of Fn the noise in imagestaken with an EM-CCD is greater than those from an ORCA-Flash4.0. Thus, when background is high, separation of signal from background in an EM-CCD image will be more difficult.
CNR also describes how we perceive the quality of the image. A good rule of thumb is that a pixel with a CNR of 2 can be detected by eye. On the low side, a pixel with a CNR of 1 can be just barely detected. However, this is a CNR for a single pixel of signal relative to background. Images with a CNR < 1 can show structures at reduced spatial or temporal resolution. When pixels of much lower CNR are grouped together, there is an effect called spatial pixel averaging.

When we look at images our brain performs complex functions including integrating large areas of similar signal, looking for patterns, symmetries and edges. For this reason, if we have a collection of adjacent pixels even with a very poor CNR (< 1), we may still be able to detect them visually.
Mathematically, visibility is improved by the square root of the number of pixels averaged.2 In a quantitative imaging experiment, measurements are made by well-defined algorithms, not by eye. But we can only view images in any publication or presentation with our eyes and therefore we must be aware of the spatial averaging or integration that is happening automatically in our brain.
Along with this automatic visual processing, images that are displayed are subject to many variables intrinsic to the display format (e.g., quality of the monitor, intensity scaling of the image data, printing technique, etc.) that can affect the perceived contrast. For these reasons, determinations of the quality of an image from a given camera should never be assessed exclusively by eye or on image files that have been subject to lossy compression, such as jpeg.
References
- Murray, J. M., Appleton, P. L., Swedlow, J. R. & Waters, J. C. Evaluating performance in three-dimensional fluorescence microscopy. J. Microsc. 228, 390–405 (2007).
- Thompson,M. (2003).
- Confirmation
-
It looks like you're in the . If this is not your location, please select the correct region or country below.
You're headed to Hamamatsu Photonics website for JP (English). If you want to view an other country's site, the optimized information will be provided by selecting options below.
In order to use this website comfortably, we use cookies. For cookie details please see our cookie policy.
- Cookie Policy
-
This website or its third-party tools use cookies, which are necessary to its functioning and required to achieve the purposes illustrated in this cookie policy. By closing the cookie warning banner, scrolling the page, clicking a link or continuing to browse otherwise, you agree to the use of cookies.
Hamamatsu uses cookies in order to enhance your experience on our website and ensure that our website functions.
You can visit this page at any time to learn more about cookies, get the most up to date information on how we use cookies and manage your cookie settings. We will not use cookies for any purpose other than the ones stated, but please note that we reserve the right to update our cookies.
1. What are cookies?
For modern websites to work according to visitor’s expectations, they need to collect certain basic information about visitors. To do this, a site will create small text files which are placed on visitor’s devices (computer or mobile) - these files are known as cookies when you access a website. Cookies are used in order to make websites function and work efficiently. Cookies are uniquely assigned to each visitor and can only be read by a web server in the domain that issued the cookie to the visitor. Cookies cannot be used to run programs or deliver viruses to a visitor’s device.
Cookies do various jobs which make the visitor’s experience of the internet much smoother and more interactive. For instance, cookies are used to remember the visitor’s preferences on sites they visit often, to remember language preference and to help navigate between pages more efficiently. Much, though not all, of the data collected is anonymous, though some of it is designed to detect browsing patterns and approximate geographical location to improve the visitor experience.
Certain type of cookies may require the data subject’s consent before storing them on the computer.
2. What are the different types of cookies?
This website uses two types of cookies:
- First party cookies. For our website, the first party cookies are controlled and maintained by Hamamatsu. No other parties have access to these cookies.
- Third party cookies. These cookies are implemented by organizations outside Hamamatsu. We do not have access to the data in these cookies, but we use these cookies to improve the overall website experience.
3. How do we use cookies?
This website uses cookies for following purposes:
- Certain cookies are necessary for our website to function. These are strictly necessary cookies and are required to enable website access, support navigation or provide relevant content. These cookies direct you to the correct region or country, and support security and ecommerce. Strictly necessary cookies also enforce your privacy preferences. Without these strictly necessary cookies, much of our website will not function.
- Analytics cookies are used to track website usage. This data enables us to improve our website usability, performance and website administration. In our analytics cookies, we do not store any personal identifying information.
- Functionality cookies. These are used to recognize you when you return to our website. This enables us to personalize our content for you, greet you by name and remember your preferences (for example, your choice of language or region).
- These cookies record your visit to our website, the pages you have visited and the links you have followed. We will use this information to make our website and the advertising displayed on it more relevant to your interests. We may also share this information with third parties for this purpose.
Cookies help us help you. Through the use of cookies, we learn what is important to our visitors and we develop and enhance website content and functionality to support your experience. Much of our website can be accessed if cookies are disabled, however certain website functions may not work. And, we believe your current and future visits will be enhanced if cookies are enabled.
4. Which cookies do we use?
There are two ways to manage cookie preferences.
- You can set your cookie preferences on your device or in your browser.
- You can set your cookie preferences at the website level.
If you don’t want to receive cookies, you can modify your browser so that it notifies you when cookies are sent to it or you can refuse cookies altogether. You can also delete cookies that have already been set.
If you wish to restrict or block web browser cookies which are set on your device then you can do this through your browser settings; the Help function within your browser should tell you how. Alternatively, you may wish to visit www.aboutcookies.org, which contains comprehensive information on how to do this on a wide variety of desktop browsers.
5. What are Internet tags and how do we use them with cookies?
Occasionally, we may use internet tags (also known as action tags, single-pixel GIFs, clear GIFs, invisible GIFs and 1-by-1 GIFs) at this site and may deploy these tags/cookies through a third-party advertising partner or a web analytical service partner which may be located and store the respective information (including your IP-address) in a foreign country. These tags/cookies are placed on both online advertisements that bring users to this site and on different pages of this site. We use this technology to measure the visitors' responses to our sites and the effectiveness of our advertising campaigns (including how many times a page is opened and which information is consulted) as well as to evaluate your use of this website. The third-party partner or the web analytical service partner may be able to collect data about visitors to our and other sites because of these internet tags/cookies, may compose reports regarding the website’s activity for us and may provide further services which are related to the use of the website and the internet. They may provide such information to other parties if there is a legal requirement that they do so, or if they hire the other parties to process information on their behalf.
If you would like more information about web tags and cookies associated with on-line advertising or to opt-out of third-party collection of this information, please visit the Network Advertising Initiative website http://www.networkadvertising.org.
6. Analytics and Advertisement Cookies
We use third-party cookies (such as Google Analytics) to track visitors on our website, to get reports about how visitors use the website and to inform, optimize and serve ads based on someone's past visits to our website.
You may opt-out of Google Analytics cookies by the websites provided by Google:
https://tools.google.com/dlpage/gaoptout?hl=en
As provided in this Privacy Policy (Article 5), you can learn more about opt-out cookies by the website provided by Network Advertising Initiative:
http://www.networkadvertising.org
We inform you that in such case you will not be able to wholly use all functions of our website.
Close